Sampling the user base

I’ve been taking a look at the users lately. I was bored, ok?

I can’t reasonably perform any graph query on the number of users the platform has, I just don’t have that kind of firepower at hand right now. So I logged in to my admin account and downloaded a sample of them. Namely, my bidirectional transitive closure, as seen from the “following” relationship.

That still makes up a nice graph of 103 699 vertices, 314 814 edges.¹ Cool data, but I’m not computing its metrology using Floyd-Warshall anytime soon.

The next best thing would be to find a cool way to display it. But that’ll need inspiration; just dumping the data to GraphViz is… unconvincing.

Wait. Directional edges being about three times the number of vertices means most people only follow a single person! Let’s get rid of them. How many is that? 28 194. Mmm, maybe those with no followers? 15 125. Is it possible my transitive closure data could, by a terrible twist of fate coupled with unbelievably bad luck, be somewhat biased?²

Ok, let’s sink to the level of social media metrics. Filter by influence, crudely approximated by number of followers. What would this look like?

1. _Royale with 1 228 followers
2. martin with 1 175 followers
3. Soc with 1 155 followers

Hurray! Bravo to the winners. 3 558 follows, we’ll be through with this in no time. Oh wait, those are follows, not followers. How many followers would that be? My inside information says 2 939. That’s a yield of 980, that could be all right. Let’s plot this.

Apart from our top few mentioned above, that data’s surprisingly regular. We can eye-regress it to: influencers = 1.32 × 10⁵ cutoff^− 1.462 and reach = 1.09 × 10⁵ cutoff^− 0.451, which simplifies to reach = 1.35 × 10¹³ influencers^0.308.

So yes, diminishing returns as expected. But at least we’re confident we can pick any number of influencers in the 100–1000 range and have it be representative. So let’s try that, with 100.³

Yeah, still pretty messy.

And what we’re measuring is rather vain: the direct number of followers. Why should we care someone has a lot of followers, if they’re from a completely very different group to ours? For example, we can notice hints of a russian and a chinese subgraph. With all due respect to them, we the rest of the world aren’t necessarily too impressed with that.

A sideways fix to that is to give the links some transitivity value. If we make the assumption that following someone grants some vague notion of trustworthyness, surely that ought to propagate in some way. The most well-known way to do that is Page and Brin’s PageRank algorithm. Here’s the top 50, ranked and compared to the simplistic following-size heuristic.

1. _Royale ↔︎
2. MadKnight ↑3
3. Magus ↑1
4. martin ↓2
5. Neumann ↑2
6. Soc ↓3
7. eulerscheZahl ↑2
8. fish2go ↑91
9. Bob ↑12
10. Agade ↓2
11. [CG]SaiksyApo ↑8
12. [CG]Maxime ↑1
13. reCurse ↑7
14. BlitzProg ↑29
15. R4N4R4M4 ↑3
16. [CG]Nonofr ↓4
17. AlkhilJohn ↓11
18. Uljahn ↑16
19. Unihedron ↑20
20. Recar ↑32
21. pb4 ↑35
22. tourist ↑131
23. Yasser ↓7
24. Luuna ↑9
25. TheNinja ↑10
26. egaetan ↑43
27. Plopx ↑14
28. BitWolf ↓11
29. Orabig ↓7
30. nicola ↓15
31. SwagColoredKitteh ↑34
32. Jeff06 ↑25
33. [CG]OlogN ↑18
34. Romka ↑79
35. [MMI]_JA ↑303
36. [MMI]_SE ↑341
37. ValNykol ↑25
38. Alain.Delpuch ↑85
39. supermassive ↓25
40. Aveuh ↑28
41. ZarthaxX ↑25
42. Manwe ↑45
43. [CG]Thibaud ↑16
44. cup_of_tea ↓6
45. inoryy ↑26
46. MathieuGanesan ↓22
47. JBM ↑38
48. Marchete ↓3
49. macqueen ↑1353
50. Fabien ↓40

Don’t get too impressed by the fact most of the changes are upwards: we are observing the top, after all. What’s more interesting are the two bubbles ranked 35 and 36, and the massive rise of rank 49.⁴ I’ll have to dig deeper there, eventually.

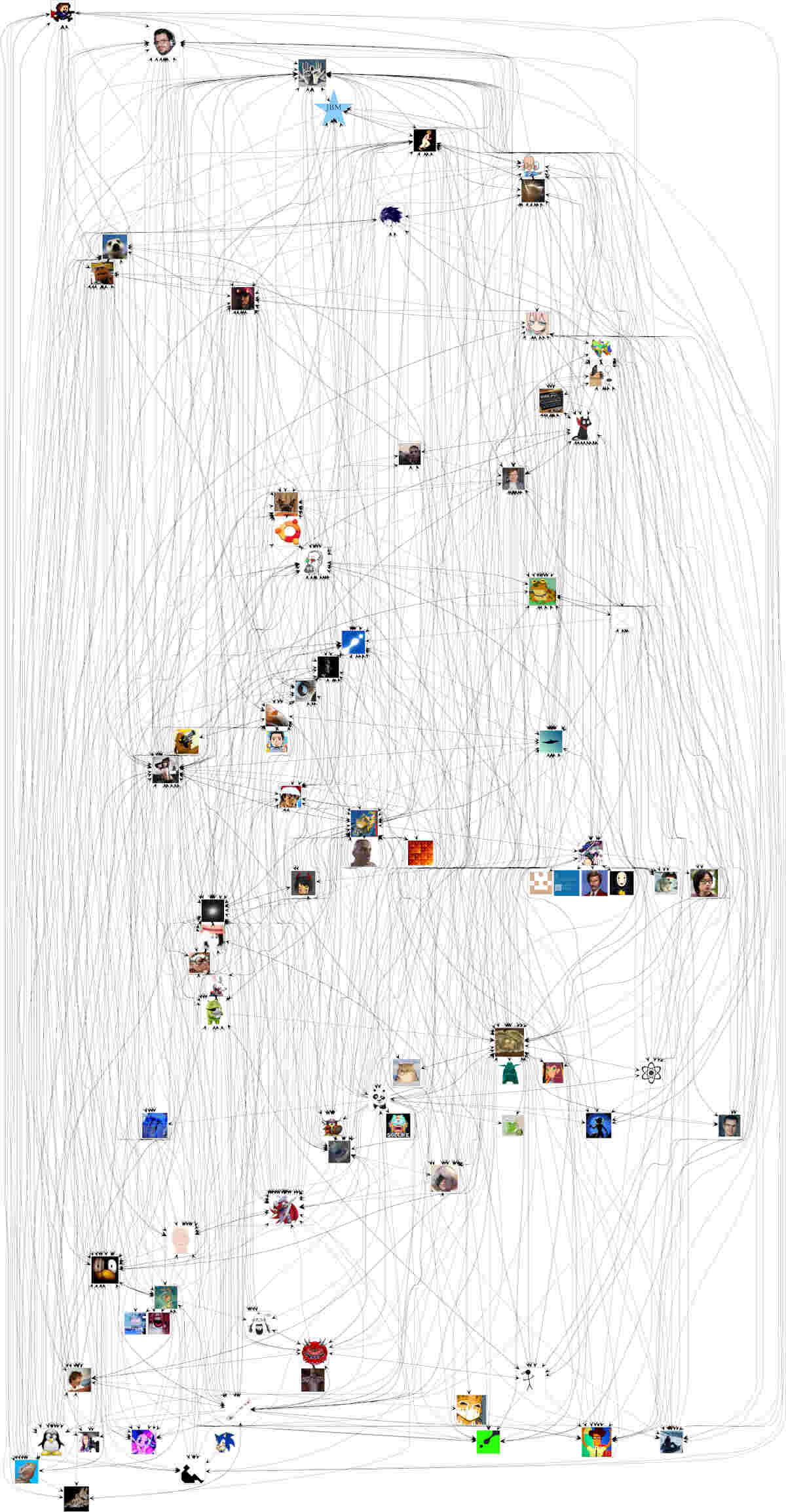
Having given some value to the links’ transitivity, we find a new hope at visualizing: edge redundancy. We can afford to drop an edge as long as the link remains. For example, we can contract the graph made of three links A→B, B→C, A→C to a single chain.

What if there are loops? We can sidestep them with PageRank too, for example by only eliminating edges that go in the same direction as their substitute.

It’s almost too good to be true.⁵

We now have a perfectly legible way of visually processing information that’s worth as much as you want it to.⁶ Victory!

Now I’ve made it abundantly clear why I don’t work at Facebook yet, let’s check some stupid factoids about the users in their glorious individualness. Echoing some #World discussion from earlier this week:

• the nickname with the most users is BrunoSilva. (Use the site’s search tool to see them. Yes, the site has a search. It’s in the middle of the top navbar.) We can only assume they date back to a time when the site didn’t check for duplicates.

• if we relax to case-insensitive collation, Alex, God, Kamikaze, Neo, NoOne⁷, Paradox, Sinner tie. Runner-ups: Anony, Blast, Dams, Rik, Soso. Hello to the Pacman, Pac-man and KingKong.

• alphabetics only? Search tool isn’t enough anymore, but I’ve got 9 Antoine, Codemaster, E, F, Ivan, J, Julien, N, Nico, No, Toto. The most interesting among rank 8: Alpha, Hunter, J/k, Math, Noname, Pi, Player, Shadow and… Thalesservices!

• that’s assuming we don’t want to count all of the anonymous together. 6 614 of them, and that’s got to be a huge underestimate with regard to the entire user base.

• a few users still have a space character in their nickname. (This isn’t possible anymore.) I have 27 of them in my set. Some even have multiple: Copy n Paste, MesmeriZing Macho Machine, [MAR] Bigtoto, Reductio Ad Absurdum, to select only those who do not appear to be using their real name.

• the country with the highest average level is Slovenia. Lowest is Vatican. Our belief in self-selected flags is just that divine.

That’ll be all. Take care!